Распределение двумерной случайной величины

[Harfangi]

Доброго времени суток!

(Оффтоп)

Это снова я и снова со случайными величинами...

Задача с переписки контрольной:

Случайная величина $\xi$ распределена равномерно на [-1;1].
Найти распределение $(\xi^2,\xi^3)$

Я ввела обозначения:
$\eta=\xi^2, \mu=\xi^3$
Задача сформулирована в точности так, как дана на контрольной. Преподаватель объяснял, что ответ на такую задачу можно дать как в виде плотности распределения, так и в виде функции распределения. Я выбрала расчет плотности распределения.

Мне удалось посчитать распределения отдельно для каждой компоненты вектора:
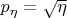
$p_{\eta}=\sqrt{\eta}$ и $ p_{\mu}=3/2 \cdot \mu^{2/3}$

Если исходить из независимости $\mu$ и $\eta$, то:
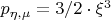
$p_{\eta,\mu} = 3/2 \cdot \xi^3$. Может ли это быть правильным ответом?

[--mS--]

По определению не пробовали?

(Оффтоп)

Неужели задача так и поставлена? Найти то, чего нет?

[Harfangi]

--mS--
по определению, это так:
$F{\eta,\mu}(x,y) = P((\eta<x),(\mu<y))$?

Я не знаю, что тут придумать, с.в. же зависимые...

(Оффтоп)

как так нет??? там сказано найти распределение, и я подумала, что можно и плотность распределения

[--mS--]

Harfangi в сообщении #963769 писал(а):

Я не знаю, что тут придумать, с.в. же зависимые...

Здесь нет никаких зависимых величин, есть одна-единственная случайная величина $\xi$. Про неё вероятности вычислять умеете?

(Оффтоп)

Harfangi в сообщении #963769 писал(а):

как так нет??? там сказано найти распределение, и я подумала, что можно и плотность распределения

Судя по всему, Вы так и не разобрались с предыдущей задачей. Ну и с этой так же не разберётесь, если не будете решать сами.

[Lia]

Тема перемещена из форума «Помогите решить / разобраться (М)» в форум «Карантин»
по следующим причинам:

- отсутствуют собственные содержательные попытки решения задач(и).

Исправьте все Ваши ошибки и сообщите об этом в теме Сообщение в карантине исправлено.
Настоятельно рекомендуется ознакомиться с темами Что такое карантин и что нужно делать, чтобы там оказаться и Правила научного форума.