"Электричество и магнетизм".
Видимо, это часть цикла "Общая физика", ещё до курсов "Уравнения математической физики" и тем более до "Теоретической физики".
Тогда во-первых, имейте в виду: стоит заглянуть вперёд.
"Электричество и магнетизм" - можно взять
Тамма. По чему бы вы ни учились, его можно использовать как справочник.
"Уравнения математической физики" - смотрите учебники
Владимирова,
Тихонова-Самарского,
Морса-Фешбаха,
Кошлякова-Глинера.
"Теоретическая физика" - библия
Ландау-Лифшиц "Теория поля" (второй том десятитомника
"Теоретическая физика").
Попробую произнести некий всеобуч на тему УМФ. "Уравнениями математической физики" называют прежде всего дифференциальные уравнения в частных производных (ДУЧП, хотя встречаются и другие уравнения, например, интегральные). В этом смысле, курс УМФ продолжает курс обыкновенных дифференциальных уравнений (ОДУ, которые тоже частенько в физике встречаются). Фундаментальные физические законы для пространства или среды обычно оказываются именно ДУЧП, а разнообразные физические явления возникают как решения этих уравнений. Чтобы ОДУ имело одно и единственное решение, необходимо фиксировать

начальных условий, где

- порядок уравнения. В УМФ используется понятие "задачи" - это уравнение + такой набор условий, которые вместе взятые дают существующее и однозначное решение (и имеется соответствующая теорема существования и единственности). В ОДУ начальные условия задаются в одной точке, когда решение вычисляется на отрезке. В ДУЧП имеется пространство нескольких независимых переменных (аргументов функции), и решение вычисляется в какой-то области этого пространства, а условия задаются на границах этой области, например, на сторонах квадрата или гранях куба.
Разнообразие ДУЧП очень велико, но УМФ интересуют только несколько типов уравнений. Образно по физическому смыслу это такие уравнения:
- стационарные уравнения (например, электростатика, или равновесие упругой плёнки);
- нестационарные уравнения, в основном таких двух типов:
- уравнения без волновых процессов (здесь различные процессы теплопроводности, диффузии);
- уравнения с волновыми процессами - волновые уравнения.
Математически понятия более чёткие, и называются уравнениями второго порядка эллиптического, параболического и гиперболического типов. Конечно, не важно, как мы назовём переменную времени, буквой

или
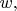
- отличия лежат в структуре уравнений.
Уравнения эллиптического типа требуют граничных условий со всех сторон области: скажем, если записано уравнение в квадрате на плоскости

то необходимо задать по одному условию на каждой стороне квадрата.
Уравнения нестационарных типов - параболические и гиперболические - требуют задания начальных и краевых условий. То есть, если записано уравнение в квадрате на плоскости

то необходимо задать условия в начальный момент времени

и условия на краях отрезка

Тогда, начиная с момента времени

уравнение покажет какие-то нестационарные процессы, например, колебания и волны, и постепенно дойдёт до момента времени

который образует другую сторону квадрата - то есть, на этой другой стороне никаких условий задавать уже не нужно.
Параболические уравнения (с первой производной  ) требуют одного условия в начальный момент времени - только
) требуют одного условия в начальный момент времени - только 
Гиперболические уравнения (с первой производной  ) требуют двух условий в начальный момент времени - и
) требуют двух условий в начальный момент времени - и 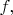 и
и 
Уравнения Максвелла - это по сути волновое уравнение. Оно посложнее, чем простейшие модельные уравнения в учебниках УМФ (типа уравнения колебаний струны), потому что оно векторное, в нём электрическое и магнитное поле, и вообще много компонент. Но по сути, уравнение такое же. И ещё, чисто в силу сложившейся традиции, уравнения Максвелла записываются не в виде уравнения второго порядка, чтобы рассматривать величину функции

и её производной

а в виде системы уравнений первого порядка. Так что, набор (электрическое поле, магнитное поле) - приблизительно соответствует этому набору
 -- 08.01.2015 17:17:25 --
-- 08.01.2015 17:17:25 --Далее:

Нет. Мы же решили, что у нас квазистационарное приближение. Значит, вообще везде надо заменять

Это пренебрежимо малые величины.
Вы, конечно, можете посчитать что-то. Но оно не состыкуется между собой. Потому что изначально решается не та задача.