Римановы суммы

[demolishka]

Имеется произвольная непрерывно дифференцируемая на отрезке $[0;1]$ функция $x(t)$. Для нее составляется сумма $\sigma_n = \sum\limits_{k=0}^{2^n-1}|x(\frac{k}{2^n})-x(\frac{k+1}{2^n})|$. Нужно обосновать существование предела

$$\lim\limits_{m \to +\infty}\frac{1}{m}\sum\limits_{n=1}^{m}\sigma_n.$$

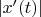
Ясно, что $\sigma_n$ это риманова сумма для $|x'(t)|$. Значит,

$$\forall \varepsilon>0 \; \exists n_0: \; \forall n>n_0 \; \left| \sigma_n - \int\limits_{0}^{1}|x'(t)|dt \right| < \varepsilon.$$

Отсюда, получаем, что для заданного $\varepsilon>0$ и достаточно большого $m$ можно выкинуть первые $n_0$ членов суммы римановых сумм и получить неравенство на предел:

$$\int\limits_{0}^{1}|x'(t)|dt - \varepsilon \leq \lim\limits_{m \to +\infty}\frac{1}{m}\sum\limits_{n=1}^{m}\sigma_n \leq \int\limits_{0}^{1}|x'(t)|dt + \varepsilon.$$

Следует ли отсюда, что $\lim\limits_{m \to +\infty}\frac{1}{m}\sum\limits_{n=1}^{m}\sigma_n = \int\limits_{0}^{1}|x'(t)|dt$? А то мне кажется, что я чего-то упустил.

[Brukvalub]

Вы упустили простейший факт: средние арифметические членов сходящейся послед-сти сходятся к тому же пределу, что и послед-сть (см. соответсвующее упражнение в Демидовиче).