Задачки на преобразование Куммера для рядов

[popolznev]

Преобразование Куммера описывается в учебниках как довольно простая штука: исследуемый ряд $\sum a_n$ представляется в виде $\sum b_n + \sum w_n$, где $b_n$ подбирается так, чтобы $b_n \sim a_n$, и сумма ряда $\sum b_n$ легко считалась бы, а ряд $\sum w_n$ сходится быстрее, чем $\sum a_n$.

Но вот в книжке Виноградовой, Олехника и Садовничего "Матанализ в задачах и упражнениях (числовые и функциональные ряды)" есть несколько упражнений на преобразование Куммера. И там фигурируют какие-то $p_n$, чью роль я не пойму (туплю).

Вот пример задачи из этого задачника:



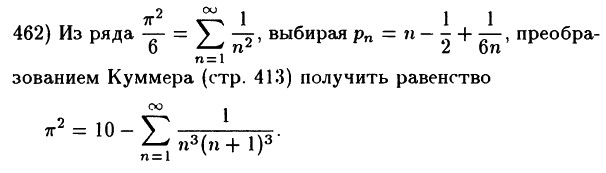
Что за $p_n$ они выбирают и как? На с. 413 написано не более того, с чего я тут начал.

Наверняка ларчик несложно открывается, но голова не варит.

[nnosipov]

Погуглите "Метод Куммера", там пример разбирается типа 462, только попроще. На загадочные $p_n$ проще не обращать внимание.

[popolznev]

Да без $p_n$-то я и сам понимаю :)

Подозреваю, они могут быть связаны с неоднократностью применения преобразования - например, $1/(n(n+1))^3$ из $1/n^2$ вряд ли получишь за один шаг.

[nnosipov]

popolznev в сообщении #953398 писал(а):

Подозреваю, они могут быть связаны с неоднократностью применения преобразования - например, $1/(n(n+1))^3$ из $1/n^2$ вряд ли получишь за один шаг.

Скорее всего. Надо остальные задачи на эту тему смотреть, чтобы понять, насколько разнообразно метод Куммера применяется.