Решить задачу оптимизации, применив теорему Куна-Таккера

min
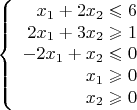
Решение:






1) первый случай

,

,


получим

,


неверно
2) второй случай

,

,


получим

,


решаем систему, получаем

так как меньше 0. исключаем этот случай из рассмотрения
3) 3 случай

,

,





получим

исключаем случай из рассмотрения
4) четвертый случай

,

,





исключаем случай из рассмотрения
5) пятый случай

,

,






исключаем этот случай
6) шестой случай

,

,





исключаем этот случай
7) седьмой случай

,

,





исключаем случай
Где ошибка в моем решении?