elena_t писал(а):
Дано множество

и

-количество всех подмножеств

. Также известна функция
![$f: 2^X \to [0,1]$ $f: 2^X \to [0,1]$](https://dxdy-01.korotkov.co.uk/f/8/e/3/8e3e928efc67aef1c46805aeb38c112882.png)
и ее свойства:
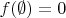


Доказать, что
![$\exists \varphi: X \to [0,1]$ $\exists \varphi: X \to [0,1]$](https://dxdy-01.korotkov.co.uk/f/c/c/5/cc576a56817788e7d4d2ef0ab694cd0f82.png)
, для какой

[/math][/math]
В качестве
![$\varphi : X\to [0,1]$ $\varphi : X\to [0,1]$](https://dxdy-03.korotkov.co.uk/f/a/9/9/a9993f1a902b9de4c9e51014a00ecf9a82.png)
годится ограничение f на одноточечные подмножества. Однако это свойство неверно для бесконечного множества X даже для бинарных отображений.