Фонарь опускается по вертикали с высоты

с постоянной скоростью

На расстоянии

расположен столб высотой

. С какой скоростью

будет двигаться конец тени, падающей от столба на землю через время

после начала движения фонаря?
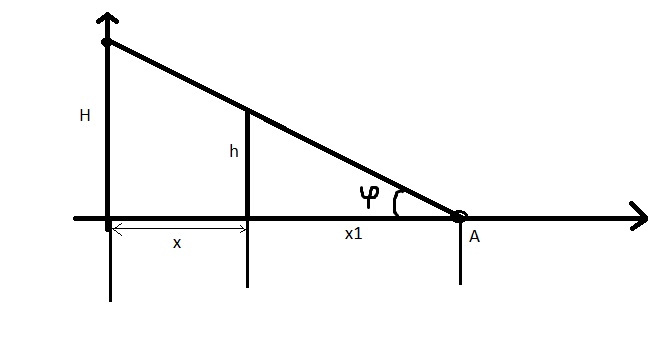
Кое- что предварительно хочу выяснить:
1) То, что я отметил на рисунке через

- это и есть длина тени столба?
2)Нужно найти измерение

за время

?
3) Когда

, точка A будет находиться на бесконечности? Ну или по крайней мере не на земле?
4) Обязательно ли, если фонарь движется равномерно, то и точка

будет так же равномерно двигаться?
Теперь, что я смог сделать из решения, я смог найти начальное положение точки

, это довольно просто:

. Ну вообще, сначала стоит найти

:

Откуда

Ну а тогда

В самом деле, если

, то положение точки

будет на бесконечности. А как мне поступить дальше, как связать все это с фонарем?
-- 13.12.2014, 22:11 --Продолжу решение, кажется, я до чего- то додумался. Пусть фонарь переместился на

и теперь он находится на высоте

. Но тогда и точка A сместится на какое- то расстояние

. Пусть новое положение точки


. Для него, по аналогии с

, можно записать:

. С другой стороны

, тогда, учитывая выражения для

и

, я получаю такой ответ:

Правильно?