Значит, текст получается такой:
Условие:На отрезке

взята точка

, а на отрезках

и

по одну сторону от прямой

построены квадраты, описанные окружности которых пересекаются в точке

. Доказать, что прямая

проходит через вершину второго квадрата и что треугольник

прямоугольный.
Решение: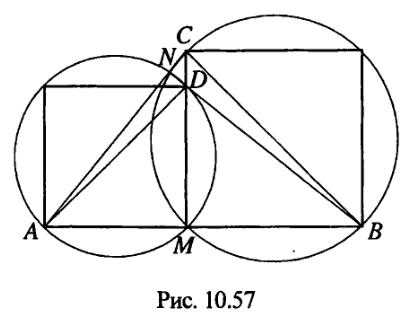
Соединим вершины квадратов

и

,

и

. Продолжим

до пересечения с

. Обозначим точку пересечения

и покажем, что она совпадает с точкой пересечения окружностей, описанных около квадратов. Действительно, так как

, то

и потому

. Но прямые углы

и

опираются на соответствующие диаметры, а значит, точка

принадлежит обеим описанным окружностям, откуда и следует доказываемое утверждение. Что и требовалось доказать.
До сих пор в этой книжке на опечатку не натыкался. Теперь всё понял. Большое спасибо.