Как доказать, что надо выбирать меньшее в данном случае?

[10110111]

Есть уравнение

$$\sin\left((\beta-1)\sqrt{\xi^2-\gamma^2}\right)\sin\xi=0,$$

где $\beta>1$ и $\gamma>0$. Интересуют решения $\xi$ Такие, что $\xi>\gamma$. Соответственно, следует выбирать подходящие из двух серий, соответствующих занулению первого и второго множителя:

$$\xi'_{n'}=\pi n',$$

$$\xi''_{n''}=\sqrt{\left(\frac{\pi n''}{\beta-1}\right)^2+\gamma^2},$$

где $n',n''\in\mathbb{Z}$. Я пытаюсь объединить эти две серии в одну так, чтобы получить явное выражение для $n$-ного корня $\xi_n$, чтобы $\xi_n>\xi_{n-1}$. Т.е. хочу найти выражение для инверсии функции "счёта корней".
Для этого определяю функцию счёта корней. Ввожу инверсии решений относительно $n$

$$\begin{align} n_1(\xi)&=\xi/\pi,\\ n_2(\xi)&=(\beta-1)\sqrt{\xi^2-\gamma^2}/\pi, \end{align}$$

и тогда функция счёта корней

$$n_r(\xi)=\lfloor n_1(\xi)\rfloor+\lfloor n_2(\xi)\rfloor.$$

Искомая функция $\xi_n$ - инверсия по отношению к $n_r(\xi)$. Чтобы её найти, я ввожу функцию, оценивающую $n_r$:

$$n'_r(\xi)=n_r(\xi)+\Delta(\xi)=n_1(\xi)+n_2(\xi),$$

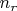
где $\Delta\in[0,2)$ - ошибка, связанная с неотброшенными дробными частями $n_1$ и $n_2$. Т.е. получается функция верхней границы для функции счёта корней. Нижнюю границу можно получить, вычтя $2$. Так выглядят три фукнции:

Теперь можно аналитически инвертировать функцию $n'_r$, решая уравнение

$$\pi n=\xi_a+(\beta-1)\sqrt{\xi_a^2-\gamma^2},$$

относительно положительной $\xi$. Решением будет

$$\xi_a=\frac{-\pi n+(\beta-1)\sqrt{(\beta-2)\beta\gamma^2+\pi^2n^2}}{\beta(\beta-2)}.$$

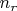
Так как $n'_r(\xi)$ является верхней границей для $n_r$, то $\xi_a$ является нижней границей для искомой $\xi(n)$. Теперь надо определить, какой же серии принадлежит искомая $\xi(n)$. Так как $\Delta<2$, то имеется только два кандидата в $n_1$ или $n_2$ (здесь округление вверх, так как $\xi$ - нижняя граница, т.е. $n_i$ может быть больше, но не меньше):

$$n_{1c}=\lceil\xi_a/\pi\rceil,$$

$$n_{2c}=\left\lceil\frac{\beta-1}{\pi}\sqrt{\xi_a^2-\gamma^2}\right\rceil=\lceil n-\xi_a/\pi\rceil.$$

Соответствующие кандидаты в $\xi$ будут тогда

$$\xi_{1c}=\pi n_{1c},$$

$$\xi_{2c}=\sqrt{\left(\frac{\pi n_{2c}}{\beta-1}\right)^2+\gamma^2}.$$

И вот самая сложность: эмпирически я обнаружил, что срабатывает такой выбор:

$$\xi=\min(\xi_{1c},\xi_{2c}).$$

Но проблема в том, что у меня не получается доказать, что этот выбор даёт точно, что соответствующий $n$ будет именно тем, который меня интересует. Т.е.

$$n=\left[\begin{align} &n_{1c}+\left\lfloor(\beta-1)\sqrt{n_{1c}^2-\frac{\gamma^2}{\pi^2}}\right\rfloor \\ &n_{2c}+\left\lfloor\sqrt{\left(\frac{n_{2c}}{\beta-1}\right)^2+\frac{\gamma^2}{\pi^2}}\right\rfloor \end{align}\right.,$$

Но какой же именно из вариантов будет-таки равен $n$ - верхний или нижний? Эмпирически выходит, что тот, который соответствует меньшему $\xi_{ic}$. Но как это доказать?