Верно ли, что решения этoго ДУ неустoйчивы по Ляпунoву?

[tetroel]

Дано ДУ $\dot{x}=t\left(x-1\right)$, $x\left(0\right)=1$

Тогда $x\left(t\right)=1+Ce^{\frac{t^2}{2}}$, $\varphi\left(t\right)=1$

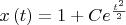
По определению $\left\lVert x\left(t_0\right)-\varphi \left(t_0\right)\right\rVert=\left\lvert x\left(0\right)-\varphi\left(0\right)\right\rvert=\left\lvert C \right\rvert$

$\left\lVert x\left(t\right)-\varphi \left(t\right)\right\rVert=\left\lvert x\left(t\right)-\varphi\left(t\right)\right\rvert=\left\lvert C \right\rvert e^{\frac{t^2}{2}}$

Далее, пусть $\delta > 0$ задано. Возьмём $\varepsilon = 1$, тогда, несмотря на выполнение $\left\lVert x\left(t_0\right)-\varphi \left(t_0\right)\right\rVert=\left\lvert x\left(0\right)-\varphi\left(0\right)\right\rvert=\left\lvert C\right\rvert < \delta$, всё равно имеет место неравенство

$\left\lVert x\left(t\right)-\varphi \left(t\right)\right\rVert=\left\lvert x\left(t\right)-\varphi\left(t\right)\right\rvert=\left\lvert C\right\rvert e^{\frac{t^2}{2}}>1$ при $t>\sqrt{2} \sqrt{\ln \left(\frac{1}{\left| C\right| }\right)}$

Следовательно, исхoдное рeшение неустoйчиво.

Для меня это дебют в этой теме, хотелось бы узнать, правильно ли я рассуждаю.

[ewert]

Правильно.