Не пойму где я неправ? Покритикуйте, пожалуйста.
Немного изменим первоначальную постановку задачи (пост от Сен 12, 2007 20:07:13):
Пусть функция

:
(1) (Нестрого) монотонно возрастает по каждому аргументу.
(2) Если

, то

для любого

.
Требуется доказать (или опровергнуть), что для любых

найдется такое

, что

.
Решение.
Обозначим
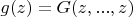
. Пусть для каких-то

неравенство
(3)

имеет место для всех

. В силу монотонности

для данных

найдется такое

, что
(4)

для любого

.
В силу (3) функция

имеет разрыв первого рода в точке

(действительно, если бы

была непрерывна в точке

, то устремив в (4)

к нулю, пролучили бы, что

).
В силу (2) и (3) имеем
(5)

для всех

и

.
В силу (2) и (4) для любого

имеем:
(6)

для любого

.
Значит функция

имеет разрыв первого рода также в точках

для всех

, то есть в каждой точке вещественной прямой. Однако, монотонная функция может иметь не более, чем счетное число разрывов первого рода. Противоречие.