Зачем для разложения этого многочлена понадобилось маленькое поле, ведь есть комплексные числа, в которых разложим любой многочлен? А мы взяли совершенно абстрактный корень этого многочлена и придумали целую алгебраическую структуру.
А многочлен не всегда задан над

. Он м.б. задан над конечным полем, над полем

-адических чисел, над полем каких-нибудь других многочленов. Обратите внимание, что расширение может быть построено над произвольным полем.
все эти маленькие поля
Они не маленькие - зависит от основного поля.
Или все это нужно затем, что находясь в некотором маленьком поле
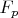
и рассматривая над ним многочлен, мы не имеет права раскладывать его в комплексных числах, потому что поле
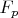
не является подполем в

? А неприводимый над

многочлен мы может разложить в

, потому что

- подполе в

?
Как бы да

Хотя я могу ошибиться тут.
Зависят ли свойства расширения поля от свойств многочлена, с помощью которого строится это расширение?
Да, размерность например.
1) Он раскладывается только на линейные множители в данном поле, а мы попытались с помощью него построить расширение. Возможно ли это?
Да. Вспомните, что такое неприводимые многочлены.
Многочлен раскладывается на линейные многочлены и некоторый неприводимый многочлен.
Еррор: текст не является утверждением.
Изменятся ли свойства расширения, построенного по этому многочлену, по сравнению с полем, построенным с помощью неприводимого многочлена? Ведь этот многочлен как бы частично неприводим, а частично раскладывается.
Есс-но.
3) Многочлен раскладывается на несколько неприводимых многочленов, то есть можно выбрать несколько корней, порождающих расширение. Что получится в данном случае? Поле, порожденное множеством корней, а не одним корнем?
Да. но при этом существует такой элемент, линейно выражающийся через корни, что полученное расширение - это простое расширение исходного поля (простое расширение - это расширение вида

, т.е. полученное добавлением одного элемента). Но это - уже не совсем тривиальная теорема.
Фактически есть всего 2 типа неизоморфных расширений: конечные (т.е. когда добавляемый элемент алгебраичен над полем) и трансцендентные (это когда построенное раширение

изоморфно полю многочленов

)
Вы можете скачать и почитать книжку Постникова Теория Галуа. Вы здесь начинаете рассуждения, почти в точности содержащиеся в 1-й главе.