Необходимо численно решить уравнение

Всё могло бы быть сделано стандартной разностной схемой для гиперболического уравнения, но дело портит перекрёстный член

.
Он даёт сразу две точки в будущем(
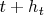
):

и

.
Соответственно, невозможно выразить одну точку в будущем (
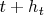
) через функции только прошлых (

). Как эту проблему решить?
(Замена переменных с аннигиляцией перекрёстного члена проблемы не решает).