Double rotation and sum of energy

[m441]

At time t=0

At time $t=0$, I rotate a grey disk or ring with a rough outer surface at angular velocity $w_1$ around the blue axis (clockwise) and at $w_2$ around the green axis (counterclockwise) as shown in the figure. $w_2$ is relative to black arm.



Now, the kinetic energy of the system is $K_E = \frac{1}{2}md^2w_1^2+\frac{1}{2}mr^2(w_1-w_2)^2$ or $K_E = \frac{1}{2}md^2w_1^2+\frac{1}{4}mr^2(w_1-w_2)^2$ (ring or disk), with $d$ the lenght of the arm, $m$ the mass of disk and $r$ radius of disk.

I built N systems like that:



**Noted blue axis are fixed to the ground.** There is friction between disks. Like black arms are turning at the same rotationnal velocity, disks are always in contact. I count all energies including the energy of friction. For simplify the study I consider friction from disk/disk give the same force F even $w_2$ decreasing, it's possible to imagine a theoretical problem or in reality it's possible to imagine oil between disks and something remove oil more and more when $w_2$ decrease. Each disk give heating $2E_1$ and like each disk is slow down its energy increase of $E_2$. I need to give energy at two last systems $2E_1$. With N systems, the sum of energy is $(N-1)2E_1+NE_2-2E_1$.

Friction can be obtain, for example, with two forces $F1/F2$: disks must be side to side. These forces don't work. An example with 2 positions at 2 diffrent times:



Only forces that need energy are magenta forces (purple). But these forces need the same energy for 3 systems than for 10 or more. In the contrary, with 10 systems, heating is higher and energy of each disk increase too.

Works of forces

$F$ is the value of green or magenta force

$w_{disks} = +N \frac{1}{2}mr^2((w_1-w_{2i})^2-(w_1-w_{2f})^2)$

with $w_{2f}<w_{2i}$
with $w_{2f}$: $w_2$ at final and $w_{2i}$: $w_2$ initial.

$W_{friction}=2(N-1)Frw_{2m}t$ with $w_{2m}$ the mean of $w_{2}$

$W_{F1}=2dF-2dF=0$
$W_{F2}=2dF-2dF=0$


$W{magentaforce}= -2Fdw_{2m}t$


$Sum=+N \frac{1}{2}mr^2((w_1-w_{2i})^2-(w_1-w_{2f})^2)+2(N-2)Frw_{2m}t$

Sum of energy

Before $t=0$, the system (N disks) has the energy $N(\frac{1}{2}md^2w_1^2+\frac{1}{4}mr^2(w_1-w_2)^2)$

At final, the system has the energy:

$$N(\frac{1}{2}md^2w_1^2+\frac{1}{4}mr^2(w_1-w_2)^2)+N \frac{1}{2}mr^2((w_1-w_{2i})^2-(w_1-w_{2f})^2)+2(N-2)Frw_{2m}t$$

My question is :

The sum of energy is not constant in this case ?

---------------------------------------------------------------

I added more cases for watch different positions of the system:






Following image shows blue axis fixed to the ground:





[1]: http://i.stack.imgur.com/6lv7v.png
[2]: http://i.stack.imgur.com/u17pO.png
[3]: http://i.stack.imgur.com/CxZwk.png
[4]: http://i.stack.imgur.com/XBexc.png
[5]: http://i.stack.imgur.com/PxFvX.png

[rustot]

I think something incorrect in initial $K_E$ calculation, for ring it must be $\frac{m (w_1^2 d^2 + w_2^2 r^2)}{2}$.

For each particle on ring $v^2 = w_1^2 d^2 + w_2^2 r^2 + 2 w_1 d\cdot w_2 r \cos(\varphi)$ and mass of each particle $dm = \frac{m d\varphi}{2\pi}$

[m441]

you're sure ? w2 is relative to black arm

[Toucan]

Тема перемещена из форума «Физика» в форум «Помогите решить / разобраться (Ф)»

[m441]

my expression is correct:

http://physics.stackexchange.com/questi ... t-a-s?lq=1

[rustot]

If it relative to arm then $w_2$ replaced to $w_2-w_1$ and expression correct. But such unusual definition of different angular velocities relative to different reference frames can be source of many hidden errors.

[m441]

what is the difference between $(w2-w1)^2$ and $(w1-w2)^2$ if the expression is a square ?

[m441]

Nobody ?

The expression of KE is correct. Sum of work seems correct. What's wrong ?

[m441]

@rustot : have you seen I wrote |w1| > |w2| in the first message (image). I don't understand your last message, kinetic energy is a function of (w1-w2)², with |w1| > |w2|, if w2 decrease the kinetic energy increase no ?

thanks for your help

[rustot]

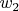
I said that with such unusual definition of $w_2$ your formula of kinetic energy is correct.

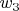
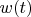
But such definition is source of potential mistakes and let me use everywhere below $w_3$ and $w(t)$ for angular speed of ring clockwise in inertial reference frame. You can at any moment replace it back to your definitions via $w_3 = w_1-w_2$

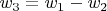
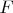
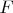
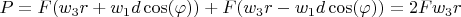
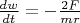
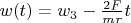
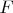
Friction $F$ for first and last ring compensated by horizontal external forces $F$, that in sum consume power $P = F (w_3 r + w_1 d \cos(\varphi)) + F (w_3 r - w_1 d \cos(\varphi)) = 2 F w_3 r$. For another intermediate rings it not competsated and each of them lose angular speed due sum of 2 friction forces. $\frac{dw}{dt} = - \frac{2 F}{m r}$, $w(t) = w_3 - \frac{2 F}{m r}t$. With fixed $F$ it will continues lineary till $w(t_0) = 0$. 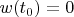From this moment there different behaviour for even and odd number of rings, but till this moment no difference and lets stop calculation at this moment $t_0 = \frac{w_3 m r}{2 F}$

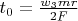
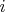
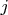
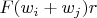
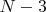
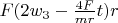
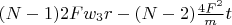
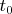
Heating power at each contact between ring $i$ and ring $j$ is $F (w_i+w_j) r$. Between intermediate rings (ie in $N-3$ contact points) it $F (2 w_3 - \frac{4 F}{m r} t) r$, and in 2 rest points it $F (2 w_3 - \frac{2 F}{m r}t)r$ and in sum $(N-1) 2 F w_3 r - (N-2) \frac{4 F^2}{m} t$. And total heating energy during $t_0$ is $(N-1) 2 F w_3 r t_0 - (N-2)\frac{2 F^2 t_0^2}{m} = N \frac{m w_3^2 r^2}{2}$

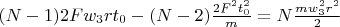
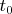
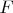
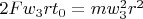
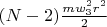
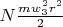
So during $t_0$ on the one hand external 2 forces $F$ did work $2 F w_3 r t_0 = m w_3^2 r^2$, intermediate rings lose $(N-2) \frac{m w_3^2 r^2}{2}$ of kinetic energy, on the other hand we got $N \frac{m w_3^2 r^2}{2}$ of heating energy. Balance is zero

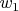
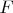
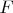
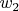
As you can see, $w_1$ finally do not affect anything. It affect for example work of upper external $F$ but affect work of lower external $F$ in opposite direction and as result do not affect summary external work. Only with strange definition of $w_2$ it can appear in final result