Требуется восстановить каноническое уравнение кривой, определить её тип и найти эксцентриситет, если фокусы кривой, если фокусы кривой

, а директрисы проходят через точки
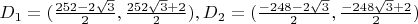
Я нашел расстояние между директрисами

и между фокусами

Можем ли мы пользоваться тем, что

и

Если так, то мы легко находим эксцентриситет, который равен

и понимаем, что это эллипс, а каноническое уравнение получим

, но если я попытаюсь найти фокусы и директрисы этого эллипса, то получу другие значения. Я так понимаю, что проблема в том, что я не учитывал центр эллипса...
Подскажите, пожалуйста, в чем ошибка (если она есть) и как подправить?