С разбором моего примера двух изоморфных рядов, какие фактор-группы изоморфны каким
Например, так



Спасибо.
Такие соотвествия мне тоже приходили в голову. Но как формально записать определение? В другом учебнике я наткнулся на такое:
Два ряда(ряды записаны по "убыванию")

и

называются изоморфными, если
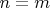
и существует такая перестановка

, что

Как мне показалось это определение неправильно, потому что в данной перестановке всегда будет(если это перестановка не идентичная) такой элемент

, что

и для

такого, что

фактор-группа

явно не будет изоморфна
