Пусть
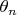
есть некая статистическая оценка параметра

. Известно, что
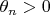
п.н. и что
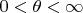
. Известно также что
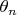
сходится по вероятности к

с ростом

, и что
![$E[\theta_n]\to\theta$ $E[\theta_n]\to\theta$](https://dxdy-01.korotkov.co.uk/f/c/8/0/c807e82388a5ae0dea490ee312fbe4b082.png)
при

.
Пусть теперь
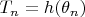
и
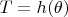
, где
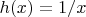
. Требуется доказать что
![$EV[T_n/T]\to1$ $EV[T_n/T]\to1$](https://dxdy-01.korotkov.co.uk/f/0/f/8/0f80a005c57813b30fb6f478690dbd0282.png)
при

.
Цепь рассуждений следующая: разложим
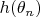
в ряд Тейлора в окрестности точки

, т.е.
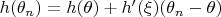
, где

лежит между
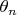
и

. Тогда имеем:
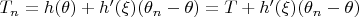
и
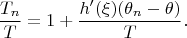
Осталось показать, что
![$E[h'(\xi)(\theta_n-\theta)]\to0$ $E[h'(\xi)(\theta_n-\theta)]\to0$](https://dxdy-01.korotkov.co.uk/f/8/d/d/8dd81df9a369ef420abefb1c441b7e4d82.png)
при

. Пытаюсь разбить это мат ожидание на две части:
![$E[h'(\xi)(\theta_n-\theta)]=E[h'(\xi)(\theta_n-\theta);\theta_n>\theta]+E[h'(\xi)(\theta_n-\theta);\theta_n<\theta]$ $E[h'(\xi)(\theta_n-\theta)]=E[h'(\xi)(\theta_n-\theta);\theta_n>\theta]+E[h'(\xi)(\theta_n-\theta);\theta_n<\theta]$](https://dxdy-04.korotkov.co.uk/f/7/f/5/7f5b796dea10aa5bddea177655a8be3282.png)
. Корректно ли сказать, что
![$E[h'(\xi)(\theta_n-\theta);\theta_n>\theta]\le0$ $E[h'(\xi)(\theta_n-\theta);\theta_n>\theta]\le0$](https://dxdy-04.korotkov.co.uk/f/3/6/4/3645731f8aec27a8ec9ecaa0822ec93982.png)
и соответственно
![$E[h'(\xi)(\theta_n-\theta)]\le E[h'(\xi)(\theta_n-\theta);\theta_n<\theta]$ $E[h'(\xi)(\theta_n-\theta)]\le E[h'(\xi)(\theta_n-\theta);\theta_n<\theta]$](https://dxdy-03.korotkov.co.uk/f/e/8/7/e87a74db004c70fc388912d6f48cd8e682.png)
и далее, что т.к.
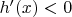
и
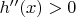
, то
![$E[h'(\xi)(\theta_n-\theta);\theta_n<\theta]\le h'(\theta)E[\theta_n-\theta;\theta_n<\theta]$ $E[h'(\xi)(\theta_n-\theta);\theta_n<\theta]\le h'(\theta)E[\theta_n-\theta;\theta_n<\theta]$](https://dxdy-04.korotkov.co.uk/f/7/8/c/78c1fdaaeba65560a25031e312e4d13b82.png)
?
И можно ли утверждать, что
![$E[\theta_n-\theta;\theta_n<\theta]\to0$ $E[\theta_n-\theta;\theta_n<\theta]\to0$](https://dxdy-04.korotkov.co.uk/f/7/1/1/711feed41e84affab02f22343d85ebf082.png)
при

?
Меня на самом деле интересует более сложная функция

, но ее поведение суть мало чем отличается от

.
Спасибо за помощь.