Задача по теории вероятностей

[Limit79]

Здравствуйте!

Имеется такая задачка:

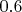
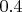
Студент на контрольной работе решает $4$ задачи с вероятностями $0.7$, $0.6$, $0.5$, $0.4$, соответственно, $1$-ю, $2$-ю, $3$-ю и $4$-ю задачи.

Сколько раз в среднем ему придется выполнять контрольную работу до зачета, если контрольная работа засчитывается при решении не менее $3$-ч задач?

Вычислите СКО числа попыток выполнить контрольную работу.

Мои мысли:

Вероятность того, что студент решит все $4$ задачи:

$$0.7 \cdot 0.6 \cdot 0.5 \cdot 0.4= 0.084$$

Вероятность того, что студент решит $3$ задачи:

$$0.7 \cdot 0.6 \cdot 0.5 \cdot 0.6 + 0.7 \cdot 0.6 \cdot 0.5 \cdot 0.4 + 0.7 \cdot 0.4 \cdot 0.5 \cdot 0.4 + 0.3 \cdot 0.6 \cdot 0.5 \cdot 0.4 = 0.302$$

Тогда вероятность того, что студент решит не менее трех задач, то есть сдаст контрольную

$$0.084+0.302 = 0.386$$

Пусть $p$ -- вероятность того, что студент сдаст контрольную, а $q$ -- вероятность того, что не сдаст, тогда:

$$p=0.386$$

$$q=1-p=1-0.386=0.614$$

Пусть дискретная случайная величина $X$ -- число попыток сдать работу, $X$ имеет геометрическое распределение.

Вероятность сдать контрольную с $m$-го раза:

$$p_{m} = P\{X=m\} = q^{m-1} \cdot p = 0.614^{m-1} \cdot 0.386$$

В среднем, число попыток, которые ему придется сделать, чтобы сдать работу -- это мат. ожидание $X$.

Для геометрического распределения, мат. ожидание равно

$$M(X) = \frac{1}{p} = \frac{1}{0.386} \approx 2.591$$

Искомое СКО:

$$\sigma = \sqrt{D(X)} = \sqrt{\frac{q}{p^2}} = \frac{\sqrt{q}}{p} = \frac{\sqrt{0.614}}{0.386} \approx 2.03$$

Собственно, вопрос: верна ли логика решения?

Смущает то, что "в среднем, число попыток, которые ему придется сделать, чтобы сдать работу" получилось числом нецелым, но ведь попытки-то -- целые числа, или это нормально, так как "в среднем"?

И еще смущает тот факт, что чем больше раз студент будет пытаться сдать работу, тем меньше будет вероятность ее сдать

Спасибо!

[Otta]

Limit79 в сообщении #921097 писал(а):

Собственно, вопрос: верна ли логика решения?

Да.

Limit79 в сообщении #921097 писал(а):

Смущает то, что "в среднем, число попыток, которые ему придется сделать, чтобы сдать работу" получилось числом нецелым, но ведь попытки-то -- целые числа, или это нормально, так как "в среднем"?

Не, не смущает. Сколько орлов в среднем выпадает, если одновременно подбросить три монеты?
Нормально.

Limit79 в сообщении #921097 писал(а):

И еще смущает тот факт, что чем больше раз студент будет пытаться сдать работу, тем меньше будет вероятность ее сдать

Не так. При каждом заходе вероятность сдать ниже, чем при предыдущем. Причем каждый раз в одно и то же число раз. А это, в частности, значит, что шанс освободиться на более ранних этапах выше.

А чтобы отвечать на тот вопрос, который Вы сами себе задали, нужно поставить его правильно: вероятность сдать к $k$-му разу. А чтобы ее посчитать, нужно просуммировать соответствующие вероятности. А сумма, понятно, будет расти, так как слагаемые положительны.

[Limit79]

Otta в сообщении #921104 писал(а):

нужно просуммировать соответствующие вероятности

Ах, точно :)

Спасибо Вам!