Здравствуйте!
Есть такая задачка:
Для функций

и

записать главную часть вида

или

при

, указать их порядки роста.
Мои мысли:
Главную часть

найдем из условия

Откуда

Данный предел будет конечным и отличным от нуля, если

, тогда

и искомая главная часть имеет вид

, порядок роста равен

.
По аналогии, для второй функции:

Данный предел будет конечным и отличным от нуля, если

, тогда

и искомая главная часть имеет вид

, порядок роста равен
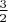
.
Подскажите, пожалуйста, мои размышления верны?
Спасибо!