You can also get a perfect score on
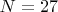
without reaching either the best minimum or maximum that has been found, since you need only have the best difference that's been found so far. It's like swimming away from a hungry shark. You do not have to be faster than the shark -- only faster than your buddy.
The (very good) upper bounds Pavlovsky presented are irrelevant to the discussion of "approaching" a perfect score. There are
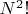
permutations of 1 to N-squared, which is finite. One of them gives the lowest Delacorte number, and one gives the highest. If someone finds the pair with the largest difference, they will have exactly one point on that sub-problem, no matter what other players have found or will find.
< Hmm - messed up the LaTeX, and not allowed to delete the message. Oh, well. >