Пусть

. В области

рассматриваем задачу





- константа. Относительно
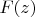
будем предполагать дифференцируемость и монотонность:

. Предположим, что

гладкая и периодическая с периодом

. Тогда у задачи существует и единственно регулярное решение из класса

.
Ниже, не оговаривая особо, мы будем пользоваться неравенством

, которое вытекает из требований на

. Отметим, что эти условия можно и ослабить.
Кроме того, ниже, чтобы не загромождать выкладки, считаем, что

.
Доказательство. Обозначим

. (На самом деле, здесь можно взять любую гладкую функцию, периодическую по

и принимающую нужные краевые условия). И ищем решение в виде

. Тогда исходное уравнение можно переписать в виде

При этом

. Для решения этого уравнения, применяем стационарный метод Галеркина.
Пусть

- базис в

,

.
Для всяких

обозначим

- подпространство, натянутое на вектора

. Далее, обозначим

-проектор на это пространство -

. Отметим, что пространство

содержит периодические по

функции, обращающиеся в 0 на краях
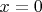
и

. Кроме того, оператор дифференцирования по

действует из

в

.
В пространстве

рассмотрим уравнение (приближение по Галеркину)

Докажем, что для некоторого

справедливо неравенство

, если только

. Тогда по лемме Вишика в шаре

найдется решение уравнения

. Очевидные преобразования дают

Отсюда

, если только норма

достаточно велика (равномерно по

).
Таким образом, решение

существует и равномерно ограничено по

. Отсюда, скорее всего, уже можно вытащить существование обобщенного решения. Но мы еще упростим нашу задачу. Для этого рассмотрим

. Как уже отмечалось,

инвариантно относительно оператора дифференцирования по

. Посему это эквивалентно действию "умножим уравнение на

и проинтегрируем по частям". Получим

Отсюда, с учетом оценки на

, получаем равномерную оценку

Обозначим найденное решение, как

.
Теперь уже можно переходить к пределу. Главная проблема - нелинейность по

. Применяем метод монотонности. Дело упрощается тем, что у нас есть оценка на

, поэтому не нужна возня со следами, при интегрировании по частям.
Итак, стандартные заклинания. Из последовательности решений

выбираем подпоследовательность, такую, что

и

и

слабо сходятся в

. Тогда сами

будут сходиться сильно в

. Речь идет о некой подпоследовательности, но этого не надо бояться (с этим мы разберемся позже).



Стандартные рассуждения из метода монотонности дают

а значит,

- решение задачи. Поскольку

, из уравнения получаем и

.
Но это сходимость какой-то подпоследовательности. А как же вся последовательность? Докажем, что и вся последовательность сходится к этому пределу. Рассуждение стандартное и опирается на теорему единственности. Как я уже показывал раньше, имеет место теорема единственности. Она нам сейчас пригодится. Итак, пусть последовательность НЕ сходится к решению. Тогда найдется некая подпоследовательность, такая , что

в

. Но применяя к ней те же самые рассуждения, получим, что из нее можно выбрать сходящуюся подпоследовательность. И сходится эта подпоследовательность к решению задачи. А оно единственно. Противоречие.
Тем самым, мы доказали, что решение существует и единственно. Последовательность приближений Галеркина сходится к решению. Правда мы лишь показали слабую сходимость производных. На самом деле, легко показать, что

сходится к

сильно в

.
Далее, если надо, требуем гладкость от

и получаем оценки на

. Отсюда получаем сильную сходимость

в

и, вроде бы, можно получить сильную сходимость в

и для

. А можно поработать со спец. базисом ( синусы в качестве

) Но, лень разбираться.