Здравствуйте.
Есть вот такое дифф. уравнение:


- решение.
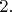
Делаю замену

и получаю

Рассматриваю случаи

.
Первый даёт

. Второй даёт

.
Заглядываю в ответы: там только

и

. Подставил

– действительно не является решением.
Собственно, вопрос вот в чём: можно ли было как-то сразу понять, что

не будет решением, или, вообще, по-хорошему
все решения просто нужно проверять подстановкой в исходное уравнение?