Выпуклая пластинка массы

катится без проскальзывания по неподвижной горизонтальной плоскости. В некоторой точке

пластинки перпендикулярно к ее плоскости прикреплен стержень длины

. Другой конец стержня неподвижно закреплен в точке

плоскости, по которой движется пластинка. Движение происходит в поле силы тяжести. Найти положения равновесия пластинки, получить условия их устойчивости и найти частоту малых колебаний пластинки в окрестности устойчивого положения равновесия. За обобщенную координату принять длину дуги

, отсчитываемую от некоторой фиксированной точки на границе пластинки до точки

соприкосновения пластинки с плоскостью. Считать, что кривизна кривизна границы в точке

- известная функция

. Моменты инерции

относительно главных центральных осей инерции

заданы. Ответ выразить через угол

, отсчитываемый от направления

до направления

и через координаты точек

и

в репере Френе

границы пластинки, вычисленные в положении равновесия.

Основная проблема возникла у меня при вычислении потенциальной энергии и положений равновесия. По вычислению кинетической энергии вопросов не возникло.
Чтобы найти положения равновесия, необходимо знать потенциальную энергию

как функцию от обобщенной координаты

, и ее критические точки. Устойчивость в этих точках, как известно, зависит от второй производной функции

.
Введем ось

перпендикулярно плоскости. Начало отсчета по оси

выберем в пересечении её с плоскостью. Тогда потенциальную энергию пластинки можно записать в виде:

,
где
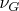
-- проекция вектора

на ось

в репере Френе

.
Чтобы найти

рассмотрим треугольник, со сторой

(см. картинку), тогда:

,
где

- проекция вектора

на ось

в репере Френе

.
В итоге, получим выражение для потенциальной энергии:

.
Далее найдем ее критические точки.

.
Правильно ли я понимаю, что положения равновесия - это все те значения

, которые удовлетворяют равенству

?
Меня немного смущает такой ответ. Можно ли как нибудь явно выразить
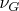
,

через

или кривизну?