Топология. Гомотопные отображения на компактном полиэдре.

[Timmy]

Всем добрый вечер.

Никак не получается следующая задача.

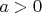
Показать, что для компактного полиэдра $X$ существует положительное число $ a>0 $ такое, что для непрерывных отображений $g, f : X \to X $, из неравенства
$\rho(f(x),g(x)) < a $, выполненного для всех точек $x$ пространства $X$, следует, что отображения $f$ и $g$ гомотопны.


Не могу сообразить из каких соображений выбрать $a$ и как именно использовать его при доказательстве.

Задача взята из следующей книги:
Ю.Г. Борисович, Н.М. Близняков, Т.М. Фоменко Введение в топологию. (стр. 396, упражнение 5)

[alcoholist]

по геодезической из $f(x)$ в $g(x)$

[Oleg Zubelevich]

я бы предложил такую общую схему. Предположим у нас имеется компакт $K\subset\mathbb{R}^m$. Причем для некоторой окрестности $U$ данного компакта имеется непрерывная ретракция $h:U\to K$. Тогда любые два достаточно близких непрерывных отображения $f_1,f_2:K\to K$ гомотопны. Гомотопия задается формулой $f_\lambda(x)=h\big((\lambda f_1(x)+(1-\lambda) f_2(x)\big),\quad 0\le\lambda\le 1$
Вместо $\mathbb{R}^m$ можно взять любое топологическое векторное пространство.

[Timmy]

Oleg Zubelevich в сообщении #895794 писал(а):

Причем для некоторой окрестности $U$ данного компакта имеется непрерывная ретракция $h:U\to K$.

А где можно прочитать о том, как данное отображение строится или про доказательство его существования?

К тому же, если я правильно понимаю, оно должно быть выпуклым или удовлетворять какому-либо другому условию для того, чтобы $\lambda f(x) + (1 - \lambda) g(x) $ лежало внутри окрестности.

[Oleg Zubelevich]

Timmy в сообщении #895878 писал(а):

где можно прочитать о том, как данное отображение строится или про доказательство его существования?

обычно это очевидно, во всяком случае уж для полиэдра построить не проблема.

Timmy в сообщении #895878 писал(а):

К тому же, если я правильно понимаю, оно должно быть выпуклым или удовлетворять какому-либо другому условию для того, чтобы $\lambda f(x) + (1 - \lambda) g(x) $ лежало внутри окрестности.

сумма лежит внутри окрестности потому, что число $\max_{x\in K}\|f(x)-g(x)\|$ мало, выпуклость не нужна

[Timmy]

Спасибо!

Про выпуклость, действительно, был не прав.