Вычисления показывают, что если среди последовательных

-и значений

нет близких к

c точностью до
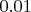
, то произведение

-и значений

, делённое на

больше

.
Покажем, как исключить значения, близкие к

c точностью до
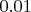
.
Пусть

- точка на эллиптической кривой

, и пусть координата

близка к

.
Тогда координата

близка к

или

.
Если она близка к

, то следующая точка в циклической группе имеет отрицательное значение первой координаты, большое по абсолютное величине, точнее тем большее, чем ближе

к

.
Следующая за этой следующей точкой близка к

.
Я проверил это при помощи следующего кода на Ubasic:
Код:
10 print "enter b: ";
20 input b
30 print "enter 1 or -1 for the sign of w";
40 input s
50 w=sqrt(b*(-b^2+10*b-5))
60 if s<0 then w=-w
70 for i=1 to 20
80 bn=(b^2-14*b+5+4*w)/(b-1)^2
90 k=(w-2)/(b-1)
100 wn=-(k*bn+2-k)
110 print bn, wn
120 b=bn:w=wn
130 next i
200 end
Если

и

, то следующая за следующей точкой равна

.
Если

и

, то следующая за следующей точкой равна

.
Если же

и

близка к

, то следующая точка близка к

, и мы получим значение

, близкое к

c точностью до
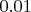
только через

c чем-то точек.
Если близкая к

точка

следует за точкой

, то произведение

имеет большое значение (большее

при

).
Таким образом, мы можем исключить точки, близкие к

и

и рассматривать произведения последовательных значений

, которые не включают значения

, близкие к

.
Исходя из вышеизложенного, доказательство роста знаменателей числа

становится делом техники и несложной компьютерной проверки.
-- Пн сен 08, 2014 10:01:10 --Исправление
-----------------
Цитата:
Необязательно брать произведение

последовательных значений

.
Произведение

значений тоже видимо всегда меньше

.
исправляется на:
Цитата:
Необязательно брать произведение

последовательных значений

.
Произведение

значений, делённое на

тоже видимо всегда больше

.