Доказать, что объём тела, образованного вращением вокруг полярной оси области

(

и

- полярные координаты), равен

.
Доказательство:
Назовём
секторной оболочкой радиуса

межу углов

и

(другого названия для данной фигуры не нашёл, поэтому придумал сам) фигуру, которую вырезают из шара радиуса

две конические поверхности, с совпадающей осью вращения, направляющие которых составляют с осью углы

и

соответственно. Тогда

. Пусть

- часть искомого объёма между лучами

и

. При очень малом
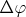
, можно считать, что

- секторная оболочка между соответствующими лучами, а значит

, из этого следует, что
, откуда следует, что искомый объём равен

.
Верно ли моё доказательство? Просьба прокомментировать его и указать на неточности, если таковые имеются.