Не. Проверяйте еще разик. Первый интервал будет не таким.
Я попробую расписать поподробней, неравенство

перепишим в более удобном виде:

Перенесем единицу влево, приведем к общему знаменателю:

Это будет верно только если и числитель и знаменатель одного знака.
То есть либо

и

либо

и

Первое неравенство дает

, а второе дает


значит остается только условие

Третье неравенство дает

, а четвертое


значит остается условие

Во втором у меня ошибка, там на самом деле будет:

или

тогда условно ряд сходится на интервале
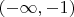
и

Для абсолютой сходимости решим неравенство

перенесем единицу вправо, приведем к общему знаменателю, получим:

Тут знаменатель всегда положителен, значит нужно искать при каких

числитель будет отрицателен. Корни уравнения -

и

а отрицателен он
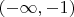
и

Окончательно получилось что область сходимости ряда:
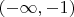
и

А область абсолютной сходимости ряда:
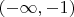
и

Вот так вот правильно?