Вы не поняли. Там используется ПРИНЯТОЕ значение. Или вычисленное принятым способом. Лично я пока (в силу моей недостаточной компетенции, разумеется) не вижу связи этого значения с реальным миром. Теоретически можно придумать другой способ вычисления, и, получив другое, близкое значение, с таким же успехом применять его.
Нет. Теоретически, если вы придумаете другой способ вычисления, он даст то же самое значение.
Если вы придумаете способ вычисления, который даст другое значение, то это будет просто способ вычисления другой величины. Не
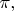
а какого-то другого числа. А оно нам бесполезно. В формулы входит именно

А в какой области электротехники или электроники (наиболее хорошо знакомыми мне) точность числа пи играет определяющую роль?
Я не говорил, что
точность играет определяющую роль. Само число

играет определяющую роль. Начиная с гармонических колебаний.
В цифровой обработке сигналов - в преобразовании Фурье, например.
Разумеется, пока вы не занимаетесь очень точными приборами и измерениями, 3-4 знаков обычно хватает за глаза. Но всё-таки не 2 знаков.
-- 28.06.2014 16:44:17 --И пишите

как формулу. Здесь на форуме так принято.