Задача такая: есть игральная кость с

гранями, на каждой число от

до

. Выпадение каждой грани равновероятно. Кость бросают несколько раз до тех пор, пока сумма очков, выпавших за все разы на кости не станет больше или равна

. Найти мат. ожидание количества бросков.
Пусть вероятность того, что игра закончится за

ходов (
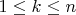
), равна

. Тогда мат. ожидание числа бросков:
![$M[k] = \sum\limits_{k=1}^nP_kk$ $M[k] = \sum\limits_{k=1}^nP_kk$](https://dxdy-01.korotkov.co.uk/f/0/1/1/01197ae676ba1cb972415b15481f1b3982.png)
.
Вероятность закончить за

ход:

.
Рассмотрим вероятность закончить за

ходов,

. Пусть за

ход было набрано

очков,

. Возможностей набрать

очков за

ход - количество разбиений числа

с

слагаемыми, что равно

. Чтобы завершить за последний ход, необходимо набрать хотя бы

очков, что можно сделать

способами. Значит, всего возможностей завершить игру за

бросков при условии, что после

бросков сумма равнялась

равно

. Всего возможностей завершить за

ходов:

. Всего по результатам

бросков возможно

исходов, значит вероятность закончить за

ходов:

.
Значит, мат. ожидание
![$M[k] = \sum\limits_{k=1}^nP_kk = \frac1n + \sum\limits_{k=2}^n\sum\limits_{l=k}^n\frac{C_{l-2}^{k-2}lk}{n^k}$ $M[k] = \sum\limits_{k=1}^nP_kk = \frac1n + \sum\limits_{k=2}^n\sum\limits_{l=k}^n\frac{C_{l-2}^{k-2}lk}{n^k}$](https://dxdy-02.korotkov.co.uk/f/1/b/5/1b5fc81ca8d10b3872e7c91d95e3d59682.png)
.
Путём нехитрых, но очень громоздких алгебраических преобразований (у меня заняли 5 страниц А4), я получил результат:
![$M[k] = \left(1+\frac1n\right)^{n-1}$ $M[k] = \left(1+\frac1n\right)^{n-1}$](https://dxdy-04.korotkov.co.uk/f/3/c/d/3cdc69d96308c926ec7e7300fd8ddd2c82.png)
.
Простота ответа подсказывает мне, что его можно было получить исходя из неких логических соображений, а не только громоздким алгебраическим способом. Можно ли эту задачу решить каким-то другим, менее громоздким способом? Спасибо.