Помогите понять доказательство.

[Anixx]

Theorem. Any entire function of order less than 1 has its Newton's expansion converging.

Proof.

Let $f$ be entire of order less than $1$, so $|f(z)|\le Ce^{|z|^p}$, $p<1$. Write the Newton polynomial

$$ P(x)=\sum_{k=0}^n\Delta^kf(0) {x \choose k} $$

Note that $g(k)=f(k)-P(k)=0$ for $k=0,1,\dots,n$. On the other hand, we can crudely estimate $|g|$ in a disk of radius $R>2n$ by $Ce^{R^p}+\sum_{k=0}^n(2R)^k\frac 1{k!}|\Delta^k f(0)|$.
Now, $\frac 1{k!}|\Delta^k f(0)|\le \max_{[0,R/2]}\frac{|f^{(k)}|}{k!}\le (2/R)^k Ce^{R^p}$ by Cauchy, so we finally get

$$ |g|\le C 4^n e^{R^p} $$

in the disk of radius $R$ centered at the origin.

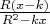
Now, for $|x|<n$, each corresponding Blaschke factor $\frac{R(x-k)}{R^2-kx}$ is at most $\frac{3n}R$ in absolute value, so

$$ |g(x)|\le C\left(\frac{12}{R/n}\right)^n e^{R^p} $$

Choosing $R=n^{1/p}$, we get $|g(x)|\le \left(12en^{-\frac{1-p}p}\right)^n\to 0$ as $n\to\infty$.

Собственно говоря, не понимаю ни хрена.

[Brukvalub]

Для начала, переведите текст на русский язык, затем последовательно задавайте вопросы по конкретным непонятным местам доказательства. Ведь изначально никто не знает, какие именно из используемых понятий и фактов вам непонятны. Может, вы не знаете, что такое интерполяционный полином Ньютона, или что такое порядок целой функции...