Странное уравнение

[Terraniux]

Найдите все значения параметра $\alpha\in \mathbb{R}$, при каждом из которых уравнение $x^\alpha + y^\alpha = z^\alpha$ разрешимо в натуральных числах.

[Legioner93]

А потом убедимся, что $\{\alpha\} \bigcap \mathbb{N}=\{1, 2\}$ и докажем ВТФ?

[fibonacci]

Я думаю $ \alpha=-1 ; 1 ; 2$

[ET]

Еще подходят все $\frac1n$ и $\frac2n$
Ps А также $-\frac1n$

[Shadow]

А также $\log_n 2$. Что за задача? Откуда?

-- 06.06.2014, 12:16 --

И вообще при любых $a,b,c \in N$ уравнение $a^x+b^x=c^x$ имеет решение.

[ET]

Shadow в сообщении #872414 писал(а):

А также $\log_n 2$.

Забавно. Меня глючит, или из ВТФ следует иррациональность этого числа?
Глючит. Тем более, что иррациональность для некоторых $n$ можно доакзать значительно проще

[Shadow]

Иррациональност этого числа при $n>2$ следует из куда более тривиального факта.
А ВТФ все таки сформулирована для целых, а не рациональных степеней.

[ET]

Shadow в сообщении #872422 писал(а):

Иррациональност этого числа при $n>2$ следует из куда более тривиального факта.

Да, я уже понял.

Shadow в сообщении #872422 писал(а):

А ВТФ все таки сформулирована для целых, а не рациональных степеней.

Я о том, что для данной задачи, как мне кажется, я перечислил все положительные рациональные решения. Вроде как то,что других положительных рациональных нет, следует из ВТФ

[Terraniux]

Shadow в сообщении #872414 писал(а):

А также $\log_n 2$. Что за задача? Откуда?

-- 06.06.2014, 12:16 --

И вообще при любых $a,b,c \in N$ уравнение $a^x+b^x=c^x$ имеет решение.

Типа пробежаться по всем тройкам и указать на $\exists$ соотв. параметра? Тогда они не будут указаны явно. Можно ли их как-либо найти в явном виде?

(Оффтоп)

Задача из головы!

[ddn]

Shadow в сообщении #872414 писал(а):

И вообще при любых $a, b, c \in N$ уравнение $a^x + b^x = c^x$ имеет решение.

Нет, для любых положительных вещественных $a, b, c$ не имеет при $min(a,b) \le c \le max(a,b)$, иначе решение существует и единствено.

ET в сообщении #872423 писал(а):

Вроде как то,что других положительных рациональных нет, следует из ВТФ

Не следует. ВТФ исключает только случаи, когда каждое $a, b, c$ это степень целого с показателем $q$ - знаменатель показателя $x = \frac{p}{q}$, $p > 3$, $gcd(p, q) = 1$.
Иначе нужна более сильная гипотеза. Ее можно еще обобщить до алгебраических степеней, т.е. кроме тривиальных $x = -\frac{1}{q}; \frac{1}{q}; \frac{2}{q}$ все другие степени трансцендентны.

Для нетривиальных степеней (не только алгебраических) те из $a^x, b^x, c^x$ будут трансцендентны у кого основание не равно $1$. Это тоже гипотеза.

Если расматривать только неприводимые $gcd(a, b, c) = 1$ и неприводимые по степени $\neg\exists(2 \le n \in \mathbb{N}) (\sqrt[n]{a}, \sqrt[n]{b}, \sqrt[n]{c} \in \mathbb{Z})$ (канонические) параметры, предполагаю что среди алгебраических останутся только решения $x = -1; 1; 2$.
Для $x = -1; 2$ все тройки уже неприводимы по степени.

Terraniux в сообщении #872604 писал(а):

Можно ли их как-либо найти в явном виде?

Нельзя, через элементарные функции и интегралы от них не выражается. Разве что перечислить тройки в порядке возрастания степени.

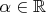
Можно усилить условие: при каких вещественных $\alpha \in \mathbb{R}$ уравнение $x^\alpha + y^\alpha = z^\alpha$ имеет несколько неприводимых решений ($gcd(x, y, z) = 1$) в натуральных числах.
Скорее всего, тогда трансцендентные степени отсеятся и выживут только тривиальные решения $\alpha = -\frac{1}{q}; \frac{1}{q}; \frac{2}{q}$, или $\alpha = -1; 1; 2$ для канонических параметров.