Площадь круга минус площадь астроиды.
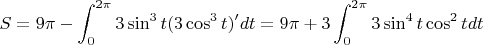
Верно ли составлен интеграл?
1) Во втором слагаемом две тройки — коэффициенты в параметрическом уравнении астроиды, и ещё одна возникает при дифференцировании, всего три тройки.
2) Площадь астроиды у Вас получается отрицательной. То, что Вы её вычитаете, это правильно, но Вы вычитаете отрицательное число:
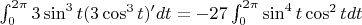
Под интегралом у Вас
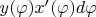
. Как это будет работать, например, в первом и втором квадранте? Здесь
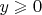
, а

убывает с ростом

, поэтому площадь, конечно, получится отрицательной.