Уважаемые математики не подскажете ли как решить номер из учебника Бермана N 3754
Пусть функция

непрерывна при

и при


стремится к конечному пределу

Доказать, при этих условиях, что если
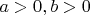
тогда
![$ \int_0^{+\infty}\frac{f(ax)-f(bx)}{x}\ dx=\left[f(+\infty)-f(0)\right] \cdot \mathrm{\ln}\frac{a}{b}$ $ \int_0^{+\infty}\frac{f(ax)-f(bx)}{x}\ dx=\left[f(+\infty)-f(0)\right] \cdot \mathrm{\ln}\frac{a}{b}$](https://dxdy-02.korotkov.co.uk/f/1/3/e/13ecddd683ac878343bfbb4026afaacb82.png)
Пытался проинтегрировать по частям, или алгебраически преобразовать – ничего не получилось. Какая здесь идея доказательства? И откуда появляется логарифм? Может здесь нужно как-то продифференцировать?