Дифф. уравнение

[Limit79]

Здравствуйте!

Подскажите, пожалуйста, как лучше понижать порядок в уравнении

$$y''=\sqrt{1+(y')^2}$$

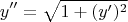
Я делаю так:

$$y'=p(y) \Rightarrow y''=p'p$$

Тогда:

$$p'p=\sqrt{1+p^2}$$

$$\frac{pdp}{\sqrt{p^2+1}}=dy$$

Интегрируя, получаю:

$$\sqrt{p^2+1} = y +C_{1}$$

Выражаю $p$:

$$p= \pm \sqrt{ (y+C_{1})^2-1}$$

Далее

$$\frac{dy}{dx}= \pm \sqrt{ (y+C_{1})^2-1}$$

$$\int \frac{dy}{\sqrt{ (y+C_{1})^2-1}}= \pm \int dx $$

$$\ln|y+C_{1} + \sqrt{ (y+C_{1})^2-1}| = \pm x + C_{2}$$

Получен общий интеграл уравнения.

Подскажите, пожалуйста, это верно?


Не хотел использовать замену $y'=p \Rightarrow y''=p'$, так как там вообще непонятно получается (не выразить явно $p$ после первого интегрирования).

Спасибо!

[Ms-dos4]

Да прям не выразить
$\[y' = u\]$

$\[u' = \sqrt {1 + {u^2}} \]$

$\[\frac{{du}}{{\sqrt {1 + {u^2}} }} = dx\]$

$\[{\mathop{\rm arsh}\nolimits} u = x + C\]$

$\[u = {\mathop{\rm sh}\nolimits} (x + C)\]$

$\[y = {\mathop{\rm ch}\nolimits} (x + {C_1}) + {C_2}\]$

(кстати, если знать гиперболические функции, решение заранее очевидно)

[Limit79]

Ms-dos4
Спасибо, забыл эту формулу

-- 27.05.2014, 02:48 --

Ms-dos4

$$\int \frac{dy}{\sqrt{ (y+C_{1})^2-1}}= \pm \int dx $$

$$\operatorname{Arch}(y+C_{1})= \pm x+C_{2} $$

$$y+C_{1}= \operatorname{ch}(\pm x+C_{2}) $$

$$y= \operatorname{ch}(\pm x+C_{2}) +C_{3}$$

У Вас:

$$y = {\mathop{\rm ch}\nolimits} (x + {C_1}) + {C_2}$$

Не могу понять, в этих двух решениях есть различие?

[provincialka]

Чосинус - четная функция.

[Limit79]

provincialka
Понял, спасибо!

[Red_Herring]

provincialka в сообщении #868249 писал(а):

Чосинус

В моём словаре шинус (sh, sinh) и кошинус (ch, cosh), и аналогично шангенс и кошангенс

[provincialka]

Red_Herring
Меня студенты научили, все претензии к ним. Впрочем "по вашему" мне больше нравится. Этот "чосинус" я никак произносить не могу.