Задача.
Даны фигуры

заданные неравенствами:

при

Найти объем тела

, являющегося объединением тел

.
Мелькнула следующая идея.
При
![$$ 0 < [x] < \exp(-\ln3/k) $$ $$ 0 < [x] < \exp(-\ln3/k) $$](https://dxdy-02.korotkov.co.uk/f/1/2/c/12ce87767bd0b5499e7266b053ad9a7882.png)
множество точек
![$F[p]$ $F[p]$](https://dxdy-01.korotkov.co.uk/f/8/b/0/8b026390148f4ab4b51f41c0ab9f6a1482.png)
, (

),
целиком содержатся в

.
Таким образом, каждопоследующее добавление - есть
(множество точек,абсцисса которых, лежит в нижеуказанных пределах)
часть тела

при

.
Попытка вычислить часть фигуры

при помощи интеграла: фиксируя

,
перенося вправо и деля на выр., получим,

, где

и

зависят от

.Но площадь этой фигуры (точнее интеграл) ,на плоскости, найти не удается.
Подстановки Чебышева не помогают.
Далее можно было бы по формуле объема
( в которой подкоренное выражение - площадь сечения,зависящая от параметра)
найти объем части
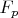
.
Есть получше идеи?
P.S. Кстати говоря эта задача предлагалась на олимпиаде "Ломоносов".
Очень сомнительно, если предполагалось, что школьники решат ее при помощи интегралов.