Условная плотность

[vlad_light]

Помогите, пожалуйста, посчитать.
Пусть $\xi \sim \mathcal U(a, b)$ и $\zeta \sim \mathcal U(-c, c)$ -- н.с.в. с равномерным распределением. Нужно посчитать $\xi \mid \xi + \zeta$.
Пусть $f_{\xi \mid \xi + \zeta}(x\mid y_0)=f_{\xi ,\xi + \zeta}(x, y_0) / f_{\xi + \zeta}(y_0)$. Найдём совместную плотность:

$$F_{\xi ,\xi + \zeta}(x, y_0)=P(\xi < x, \xi + \zeta < y_0)=\int _{-\infty }^{x}f_\xi (z)F_\zeta (y_0-z)dz\Rightarrow f_{\xi ,\xi + \zeta}(x, y_0)=f_\xi (x)f_\zeta (y_0-x)$$

Теперь найдём распределение суммы:

$$f_{\xi +\zeta }(y_0)=\int _\mathbb Rf_\xi (x)f_\zeta (y_0-x)dx$$

Тогда условное распределение будет иметь вид:

$$\frac {f_\xi (x)f_\zeta (y_0-x)} {\int _\mathbb Rf_\xi (x)f_\zeta (y_0-x)dx}$$

Посчитаем в явном виде:

$$f_\xi (x)f_\zeta (y_0-x)=\frac {1}{b-a}\chi _{(a, b)}(x)\frac {1}{2c}\chi _{(-c ,c )}(y_0 -x)$$

$$\int _\mathbb Rf_\xi (x)f_\zeta (y_0-x)dx=\int _\mathbb R\frac {1}{b-a}\chi _{(a, b)}(x)\frac {1}{2c}\chi _{(-c ,c )}(y_0 -x)dx=\frac {1}{2c(b-a)}\int _\mathbb R \chi _{(a, b)}(x)\chi _{(y_0-c, y_0+c)}(x)dx=$$

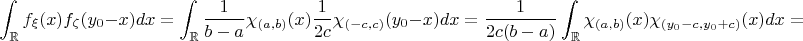
$$=\frac {1}{2c(b-a)}[(b-y_0+c)\chi _{(a+c, \infty)}(y_0)\chi _{(b-c, b+c)}(y_0)+ (y_0+c-a)\chi _{(-\infty ,b-c)}(y_0)\chi _{(a-c, a+c)}(y_0)+$$

$$+(b-a)\chi _{(-\infty, a+c)}(y_0)\chi _{(b-c, \infty )}(y_0)]$$

Правильно ли я посчитал и можно ли это как-нибудь упростить?

[--mS--]

Ну плотность суммы, конечно, можно записать безо всяких индикаторов, и числитель тоже, и поделить одно на другое. Например, при $2c<b-a$

$$f_{\xi+\zeta}(y_0) = \begin{cases}\dfrac{y_0-a+c}{2c(b-a)}, & a-c < y_0 < a+c, \cr \vphantom{\displaystyle\int_1^1}\dfrac{1}{b-a}, & a+c<y_0<b-c, \cr \vphantom{\displaystyle\int_1^1}\dfrac{b+c-y_0}{2c(b-a)}, & b-c<y_0<b+c, \end{cases}$$

а при $2c>b-a$

$$f_{\xi+\zeta}(y_0) = \begin{cases}\dfrac{y_0-a+c}{2c(b-a)}, & a-c < y_0 < b-c, \cr \vphantom{\displaystyle\int_1^1}\dfrac{1}{2c}, & b-c<y_0<a+c, \cr \vphantom{\displaystyle\int_1^1}\dfrac{b+c-y_0}{2c(b-a)}, & a+c<y_0<b+c. \end{cases}$$

[vlad_light]

Спасибо! Кстати, я так и делал, а уже потом всё через индикаторы переписал
А в совместной плотности, кроме длины отрезков, больше ничего сокращаться не должно? А то в такой громоздкой формуле этот как-то не очевидно.

[--mS--]

Да нет, не должно.