Давайте подумаем. Что мы имеем: матрицу
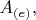
матрицу перехода

матрицу перехода

Попробуем составить выражение того, что нам нужно:

Теперь "упростите выражение". Причём имеем в виду, что операция произведения матриц - сравнительно "лёгкая", а операция взятия обратной матрицы - более "тяжёлая".
Хм-м-м, а особо-то и не упрощается. Можно, разве что, так:

Сэкономили одно умножение, но всё равно имеем два обращения. Обойтись одним обращением не знаю как.