Как доказать вариант теоремы Бэра

[Leox]

Пусть $X$ — полное метрическое пространство, $\{X_n \}_{n \in \mathbb{N}}$ — счетный набор замкнутых подмножеств $X$ причем $ {\rm int} X_n = \emptyset$, $\forall n \in \mathbb{N}$. Доказать , что ${\rm int}\, \bigcup_{n=1}^\infty X_n = \emptyset $.

Не могу адаптировать стандартное доказательство.

[Someone]

А что там адаптировать-то? Переписать один к одному, и всех делов.
Или Вы что под "стандартным доказательством" подразумеваете?

[Leox]

да, переписал, спасибо :)

[Oleg Zubelevich]

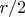
Предположим, что $V={\rm int}\, \bigcup_{n=1}^\infty X_n \ne \emptyset $. Это значит, что $V$ содержит открытый шар радиуса $r>0$, а внутри этого открытого шара возьмем замкнутый шар $B$ радиуса $r/2$. Этот замкнутый шар является полным метрическим пространством и одновременно он является объединением счетного количества замкнутых множеств без внутренних точек $X_n\cap B$. Противоречие с теоремой Бэра.

[Oleg Zubelevich]

что-то тут не то с моим доказательством

[Oleg Zubelevich]

не-а все так