Пусть

вероятностное пространство. Пусть

- дискретная случайная величина, которая принимает значения на множестве неотрицательных целых чисел. Далее, пусть
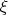
случайная величина которая равномерна распределена на

а) Записать формулу для

.
б) Доказать, что

Меня смущают слова "случайная величина которая равномерно распределена на конечном множестве". Правильно ли я понимаю, что тогда

, если
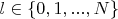
и

иначе?
Тогда для пункта а) получим:


.
Верно?
Тогда пункт б) доказывается перестановкой сумм и суммированием по

?