Конечно, они неправы, радиус должен был получиться больше радиуса первой окружности, а получился меньше.
Спасибо.
А в чем у них ошибка, интересно? Не получилось найти... Только уравнение неверно решили (точнее один из корней -- неверный). Но взяли корень
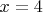
они для дальнейшего рассуждения (что походу верно, если правильно решить уравнение), но должна быть еще одна ошибка.