Свойства формального частного

[kisupov]

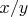
Здравствуйте. Пусть даны целые $x,y \in \mathbb{Z}/p\mathbb{Z}$, и пусть $y$ обратимо, то есть существует мультипликативная инверсия $y^{-1}$. Формальное частное $q = xy^{-1}$. Причем, если $x$ кратно $y$, то $q=x/y$. С этим все ясно. Но вот как связано формальное частное с истинным частным $x/y$, округленным до целого в ту или иную сторону, в случае, если $x$ не кратно $y$? Например, если $p$ --- нечетное число (не обязательно простое), и $y = 2$, то $\lfloor x / y \rfloor = q - \frac{p+1}{2}$ (для нечетного $x$). А есть ли какие-нибудь обобщения для случая $y \ne 2$ ? В книгах Виноградова и Айерлэнда не нашел этого. И вообще, подскажите, пожалуйста, литературу, в которой рассматривается формальное частное и его свойства.