Да, правильно. Вот ещё один способ, идейно близкий к задаче
из соседней темы.
Функция ненулевая — существует вектор

. Пусть

. Тогда

.
Возьмем произвольный вектор

. Построим комбинацию

. Чему равно значение функции

на этой комбинации?

Следовательно,

. Следовательно, любой вектор

есть линейная комбинация

и некоторого вектора из
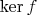
.
(Оффтоп)
Такое разложение единственно (в противном случае получили бы

). Значит,

— это к соседней задаче.
Но в
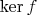
можно построить базис

. Значение функции

на этих базисных векторах равно нулю, а все векторы

образуют базис

.