Найти сопротивление бесконечной цепочки звеньев. 8 класс.

[melnikoff]

Задачка для 8 класса сразу после изучения закона Ома для участка цепи, закона Джоуля-Ленца и рассмотрения последовательного и параллельного соединения элементов цепи.
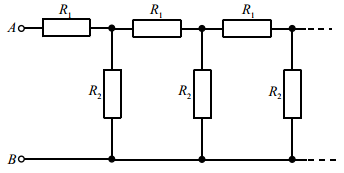
Найти сопротивление $R_{AB}=\tilde{R}_\infty$ между точками $A$ и $B$, если количество звеньев в цепи очень велико, то есть цепочка бесконечная. $R_1=3\,\text{Ом}$, $R_2=6\,\text{Ом}$.



Моя попытка:
$\tilde{R}_1=R_1+R_2$,
$\tilde{R}_2=R_1+\frac{R_2\cdot \tilde{R}_1}{R_2+\tilde{R}_1}$,
$\tilde{R}_3=R_1+\frac{R_2\cdot \tilde{R}_2}{R_2+\tilde{R}_2}$,
...........................
$\tilde{R}_n=R_1+\frac{R_2\cdot \tilde{R}_{n-1}}{R_2+\tilde{R}_{n-1}}$.

И тут ступор. Вижу, что если выражение для $\tilde{R}_1$ подставить в $\tilde{R}_2$, затем выражение для $\tilde{R}_2$ подставить в $\tilde{R}_3$ и так далее, то получится что-то наподобие бесконечной цепной дроби. Однако решение предполагается точно не такое.
Направьте в нужное русло.

[svv]

А, классика.

Подсказка: если добавить ещё одно звено, ничего не изменится.

Кстати, и для бесконечной периодической цепной дроби, не связанной с этой задачей, такой прием тоже подходит.

[melnikoff]

svv в сообщении #844358 писал(а):

Подсказка: если добавить ещё одно звено, ничего не изменится.

$R_1+\frac{R_2 R_{AB}}{R_2+R_{AB}}=R_{AB}$
$R_{AB}^2-R_1 R_{AB}-R_1R_2=0$
$R_{AB}=\frac{R_1+\sqrt{R_1^2+4R_1R_2}}{2}=6\,\text{Ом}.$

Интересно, а можно ли решить задачку тем путем, которым я начал?

[svv]

Да, правильно. Проверка: есть двухполюсник, с сопротивлением $6\,\text{Ом}$. Соединяем его параллельно с сопротивлением $R_2=6\,\text{Ом}$. Сопротивление стало $3\,\text{Ом}$. Соединяем последовательно с $R_1=3\,\text{Ом}$. Стало опять $6\,\text{Ом}$.

Понравился принцип?

-- Вт апр 01, 2014 22:45:35 --

melnikoff в сообщении #844360 писал(а):

Интересно, а можно ли решить задачку тем путем, которым я начал?

Да, конечно. В формуле
$\tilde{R}_n=R_1+\frac{R_2\cdot \tilde{R}_{n-1}}{R_2+\tilde{R}_{n-1}}$
вместо $\tilde{R}_n$ и $\tilde{R}_{n-1}$ подставьте $R_{\infty}$.
Или это нечестно? Но значение бесконечных периодических цепных дробей так и находится:
$R_{\infty}=R_1+\dfrac{1}{\dfrac 1 R_2+\dfrac 1{R_1+\dfrac{1}{\dfrac 1 R_2+...}}}$
$R_{\infty}=R_1+\dfrac{1}{\dfrac 1 R_2+\dfrac 1{R_{\infty}}}$

[melnikoff]

svv в сообщении #844363 писал(а):

Да, правильно. Проверка: есть двухполюсник, с сопротивлением $6\,\text{Ом}$. Соединяем его параллельно с сопротивлением $R_2=6\,\text{Ом}$. Сопротивление стало $3\,\text{Ом}$. Соединяем последовательно с $R_1=3\,\text{Ом}$. Стало опять $6\,\text{Ом}$.

Понравился принцип?

Да, все предельно просто оказывается.

-- 02.04.2014, 01:50 --

svv, спасибо за помощь!

[svv]

Рад был помочь.

[OlegCh]

Да, классика... Хорошая задачка с красивым решением.
Вот есть ещё другая классика - найти сопротивление бесконечной плоской решетки между соседними узлами, если собственное сопротивление каждого ребра R. И обычно приводится ее классическое решение, но оно, на мой взгляд, не совсем корректно (точнее, совсем даже некорректно!), хотя и приводит к правильному результату...

[Munin]

svv в сообщении #844363 писал(а):

Но значение бесконечных периодических цепных дробей так и находится

А вот как находится значение непериодических цепных дробей? Для меня это всегда было загадка...