Добрый день!
Читаю одну книгу и прошу помощи с непонятным отрывком. Чтобы ничего не переврать, вот отрывок на языке оригинала:
Consider
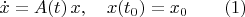
where
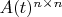
is a piecewise continuouse function belonging to
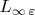
.
Далее идут некоторые определения, а затем
Note that linear systems with
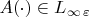
automatically satisfy the Lipschitz condition over any finite time interval, so that the solutions of (1) are unique on any time interval.
Мне не понятно - если
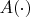
- кусочно-непрерывная, то она ведь допускает разрывы на границах интервалов, так? Как она тогда может быть Липшицевой? Объясните, пожалуйста.