Пять одинаковых лампочек соединены в цепь и подключены к источнику напряжения (см. рис.). На сколько процентов изменится мощность, выделяющаяся в этой цепи, если лампочка 1 перегорит?
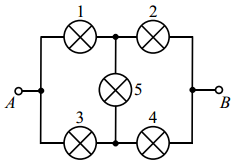
Всегда было интересно как правильно обосновывать и словесно оформлять соображения симметрии. Например, какие слова и в какой последовательности говорить, что бы убедить школьника в том, что когда все лампочки работают, то лампочка №5 гореть не будет?
Решение:
До:

После:

