Конечно, будет являться асимптотой.
Я на всякий случай спросил.
В этих 4-ёх параметрических уравнениях нужно использовать только действительные переменные и действительные коэффициенты или необходимо записать систему уравнений с использованием комплексных переменных и комплексных коэффициентов?
Странный вопрос. Если мы уже отождествили
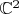
с

, зачем нам еще в 2 раза увеличивать размерность?
Хорошо, если уж очень хочется ввести асимптоты для графиков функции комплексной переменной, то можно попробовать определить так: прямая в

, такая что расстояние от точки на ней до графика стремится к нулю при стремлении параметра прямой к

или

.
В качестве бонуса: если функция алгебраическая, то число точек пересечения с графиком будет либо конечным (тогда можно заменить прямую на луч, не пересекающийся с графиком), либо отрезок прямой будет лежать на графике. В последнем случае функция может быть только линейной (принцип аналитического продолжения). Если функция не алгебраическая, то возможна ситуация вроде

.
Но опять же возникает вопрос "зачем"? Как мне кажется, цель конструкций в книге Александрова – рассказать про асимптоты квадрик без использования понятия предела. Поскольку данная тема происходит из анализа, нет никакого смысла его избегать. А в анализе часто намного удобнее сразу говорить про асимптотические разложения.