Нет, от ранга

зависит размерность

плоскости, которую составляют решения

системы

.

Пусть система совместна (ранг

основной матрицы равен рангу расширенной).
Тогда при ранге

размерность будет

.

Пусть, далее, все уравнения независимы, ни одно не является следствием остальных.
Тогда ранг

, т.е. количеству уравнений.
Если уравнений

, то обязательно будут зависимые, мы этот случай исключили.
Если уравнений

, то будет единственное решение, точка. Размерность равна нулю.
Если уравнений

, то будет прямая решений. Размерность равна

.
...
Если уравнений

, то будет гиперплоскость решений, размерности

.
Это всё еще без учета ограничений

Ну, а ограниченность многогранника зависит не от ранга матрицы

, т.е. размерности

плоскости решений, а от расположения плоскости относительно системы координат. Наглядно — от того, как она сдвинута-повернута. Если хоть один её касательный вектор

имеет все неотрицательные координаты, многогранник неограничен: двигаясь по этому направлению, мы никогда не встретим никакую координатную гиперплоскость
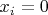
.