Отрицательные индексы

[OlgaD]

Я немного зарешалась. Подскажите, пожалуйста, если у меня есть ряд

$$\sum\limits_{n=1}^{\infty}\frac{2^n}{z^n},$$

то как его записать в виде

$$\sum\limits_{m=-\infty}^{-1}(?)\cdot z^m.$$

Зациклило, не могу сообразить, изменяется ли коэффициент.

И вообще, $c_{-n}=1/c_n?$

А вообще, наверное, проще расписать оба ряда...

[Otta]

Ну сделайте замену индекса подходящую.

-- 16.03.2014, 19:57 --

OlgaD в сообщении #837509 писал(а):

И вообще, $c_{-n}=1/c_n?$

Нет, конечно.
Какое отношение коэффициенты при положительных степенях имеют к коэффициентам при отрицательных?

[OlgaD]

Да я уж и сама поняла, что наврала

[OlgaD]

Тогда правильно ли я понимаю решение следующей задачи:

необходимо найти область сходимости ряда $\sum\limits_{n=-\infty}^{\infty}\frac{z^n}{2^n}.$

Разбиваю ряд на главную и правильную части $\sum\limits_{n=-\infty}^{-1}\frac{z^n}{2^n}+\sum\limits_{n=-\infty}^{\infty}\frac{z^n}{2^n}.$ Радиус сходимости для правильной части равен 2, т.е. $|z|<2.$ А главную часть можно переписать в виде $\sum\limits_{n=1}^{\infty}\frac{2^n}{z^n}$ и, следовательно, $c_{-n}=2^n$ и $r=\lim\limits_{n-\infty}\sqrt[n]{2^n}=2,$ т.е. $1/|z|<1/2,$ т.е. 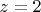$|z|>2.$ Так как при $z=2$ оба ряда расходятся, то область сходимости пустая?

[Otta]

Правильно.

[OlgaD]

Ну, значит, таки разобралась. Именно это я и хотела выяснить о $c_{-n}.$
Спасибо.