Жорданов базис

[MestnyBomzh]

Кому не трудно-проверьте решение, спасибо!
Требуется найти Жорданов базис:

$$\begin{pmatrix} 1 & 2& 1\\ 0& -1& 0\\ -4& -4& -3 \end{pmatrix}$$

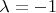
Нашел собственное число: $\lambda=-1$, кратности $3$. Нахожу собственные вектора:

$$ \begin{pmatrix} 2 & 2& 1\\ 0& 0& 0\\ -4& -4& -2 \end{pmatrix}\cdot \begin{pmatrix} h_1\\ h_2\\ h_3\\ \end{pmatrix}=\begin{pmatrix} 0\\ 0\\ 0 \end{pmatrix}$$

Нахожу базисные вектора:

$$\begin{pmatrix} -1\\ 0\\ 2 \end{pmatrix}$$

и

$$\begin{pmatrix} -2\\ 2\\ 0 \end{pmatrix}$$

Теперь нахожу присоединенный вектор:

$$\begin{pmatrix} 2 & 2& 1\\ 0& 0& 0\\ -4& -4& -2 \end{pmatrix}\cdot \begin{pmatrix} h_1\\ h_2\\ h_3\\ \end{pmatrix}=\alpha\begin{bmatrix} -1\\ 0\\ 2 \end{bmatrix}+\beta\begin{bmatrix} -2\\ 2\\ 0 \end{bmatrix}$$

. Выбираем $\alpha,\beta$ так, чтобы система имела решения. Пусть $\alpha=0,\beta=0$, тогда берем частное решение, например

$$\begin{pmatrix} 1\\ 1\\ -4 \end{pmatrix}$$

. Таким образом, Жорданов базис:

$$\begin{pmatrix} -1\\ 0\\ 2 \end{pmatrix} \begin{pmatrix} -2\\ 2\\ 0 \end{pmatrix} \begin{pmatrix} 1\\ 1\\ -4 \end{pmatrix}$$

[SpBTimes]

Как это, и альфа, и бета нули?

[MestnyBomzh]

А так нельзя?

[Nemiroff]

У вас получился не базис. Что неудивительно --- вы искали собственные векторы вместо присоединённых.

-- Сб мар 15, 2014 15:56:46 --

MestnyBomzh в сообщении #837150 писал(а):

А так нельзя?

А откуда вы это вообще взяли?

[SpBTimes]

MestnyBomzh в сообщении #837150 писал(а):

А так нельзя?

Ваше частное решение ЛЗ с собственными векторами. Догадайтесь почему.

[MestnyBomzh]

Кажется понял, потому что я пришел к тем же собственным векторам...И брал частное решение из того уравнения, из которого и уже взял 2 базисных

[SpBTimes]

MestnyBomzh
Ну так выберите нетривиальные альфа и бета