Интересная задача

[hello19]

Привет, форумчане!
Столкнулся с интересной задачей игры против некоторого робота. Игра устроена так:
Подкидывается монетка. Дальше игрок делает ставку и называет одну из возможных сторон монетки(орел или решка). Если он угадывает, то получает свою ставку, нет - проигрывает.

Хотелось бы знать, какой стратегией стоит руководствоваться в такой игре, чтобы оставаться в плюсе.

Пока только придумал такой алгоритм: Все начинается с минимальной ставки.
Если проиграли, то ставим ставку большую предыдущей в 2 раза, снова подбрасывается монета и снова угадываем сторону. Повторяем эту процедуру
Если выиграли, то ставим опять минимальную ставку.

В целом, эта стратегия приносит больше выигрыша, чем проигрыша, за исключением редких случаев, когда, например, за k удвоений (кол-во удвоений ограничено своим бюджетом)не удалось выиграть и со счета списывается сумма равная сумме геометрической прогрессии с множетелем 2.

Возможно ли как-то улучшить эту стратегию или, быть может, есть стратегия лучше?

[galenin]

А на компе пробовали такую модель прокрутить?

[hello19]

Да, конечно..
Некоторый заморский сервер играет роль того, кто подкидывает монетку, а я играю с ним через доступный API.

[kp9r4d]

Разве матожидание выигранного не будет 0 вне зависимости от ставки?

[svv]

http://ru.wikipedia.org/?oldid=60685919

Цитата:

Используя систему мартингейла, игрок не получает преимущества, он всего лишь перераспределяет свой выигрыш. Игрок проигрывает редко, но помногу, а выигрывает часто, но помалу.

Так что оптимальная стратегия — замените коэффициент 2 на 10 и увеличьте бюджет до бесконечного. Не можете или правила не позволяют? Что ж, очень жаль...

[hello19]

В том то и дело, что бюджет не позволяет устремляться до бесконечности.. Матожидание действительно нулевое
Я вот думал, что, может, используя какие-то модификации этого алгоритма можно будет хоть как-то оставаться в плюсе.. хотя, быть может, это несбыточная мечта..

Можно ли еще что-то придумать или где-то почитать про это дело?

Кроме того, можно договориться с сервером и сделать вероятность выигрыша любой из отрезка [5%-95%]. Однако, чем больше вероятность выигрыша, тем выигрыш меньше

[kp9r4d]

hello19 в сообщении #835254 писал(а):

В том то и дело, что бюджет не позволяет устремляться до бесконечности.. Матожидание действительно нулевое
Я вот думал, что, может, используя какие-то модификации этого алгоритма можно будет хоть как-то оставаться в плюсе.. хотя, быть может, это несбыточная мечта..

Можно ли еще что-то придумать или где-то почитать про это дело?

Ещё будучи школьником я очень этой задачей интересовался и лишь по одной причине — мне хотелось обмануть казино. :3 Сдается мне, что тот самый «некоторый заморский сервер» — это далеко не учебный интерактор, а какой-нибудь лохотрон. Нет, ничего придумать соблюдая правила игры нельзя, а они ещё и ГПСЧ подкрутят так, что там матожидание будет ещё и отрицательным; так что бросайте вы это.

[hello19]

Да нет, как раз тут все безопаснее, просто прохожу курс на MOOC и там есть задание на "подумать и разобраться"...
Если бы это был лохотрон, уже бы в трусах сидел)

[kp9r4d]

hello19
Хм, а выигрыш снижается/увеличивается в зависиомсти от вероятности линейно?
Я про:

Цитата:

Кроме того, можно договориться с сервером и сделать вероятность выигрыша любой из отрезка [5%-95%]. Однако, чем больше вероятность выигрыша, тем выигрыш меньше

[svv]

Решил сейчас поискать, не использует ли кто-то стратегию мартингейла (по-моему, самоубийственную) на Форексе. Оказывается, используют.

Цитата:

Торговая система Мартингейл — основана на популярной системе для ставок во Франции XVIII века. Главный принцип этой системы — это удвоение ставки после каждого проигрыша, таким образом, если вы выигрываете (получаете свою ставку плюс 100% выигрыш), вы восполняете все потери и также зарабатываете объем начальной ставки. Если бы у кого-то было бесконечное количество денег, эта стратегия была бы беспроигрышным вариантом, так как при бесконечном количестве ставок вероятность выиграть в один из исходов была бы равна 1. Проблема в том, что ни у одного трейдера нет бесконечного количества денег и, поэтому эта стратегия приводит только к расходованию всего депозита. И, хотя эта стратегия очень популярна среди Форекс трейдеров и используется во многих платных экспертных советниках для рынка Форекс, я сильно не рекомендую использовать ее.
Особенности
$\bullet$ Теоретически беспроигрышная система.
$\bullet$ Практически бесполезная.
$\bullet$ Соотношения выигрыша к ставке может достигать очень низких уровней.

Это отсюда:
http://www.earnforex.com/ru/форекс-стратегии/торговая-система-мартингейл

В общем, как увидите/услышите это слово — держитесь подальше.

[Joker_vD]

hello19 в сообщении #835224 писал(а):

Хотелось бы знать, какой стратегией стоит руководствоваться в такой игре, чтобы оставаться в плюсе.

Не играть. Как насчет партии в шахматы?

Против стратегии с удвоением ставки есть замечательный прием (и он во всех казино используется) — именно, максимальный размер ставки. И все.

[Евгений Машеров]

Стратегия известная, называется "мартингэйл" (связь с одним математическим понятием установите сами). Однако того факта, что 0=0, она не отменяет. Матожидание дохода неизменно, хотя вероятность проигрыша может быть сделана сколь угодно малой (просто сам проигрыш становится больше). Ограничивается ставка в казино не оттого, что так можно обыграть казино, а потому, что при очень большом проигрыше возможны попытки его отсудить (скажем, заявляя, что игрок был не в здравом уме, и казино должно было его не допускать), безнадёжные, но вовлекающие казино в дополнительные судебные расходы и создающие плохой пиар, а если играл в долг - то возможно банкротство игрока и получение только части проигрыша.
Это стратегия (и более осторожная "усреднение убытков", когда проигрыш по какой-то бумаге влечёт дополнительные вложения в неё же, чтобы если она вырастет - показать по ней положительный средний доход и не оправдяваться перед инвестором) довольно популярна и неоднократно применялась. Скажем, Ник Лисон именно с помощью её сперва заслужил репутацию гениального трейдера и грандиозные бонусы, а затем разорил английскую королеву и уничтожил старейший банк Англии, а для себя добыл 5 лет тюрьмы и туберкулёз.

[hello19]

Joker_vD в сообщении #835354 писал(а):

hello19 в сообщении #835224 писал(а):

Хотелось бы знать, какой стратегией стоит руководствоваться в такой игре, чтобы оставаться в плюсе.

Не играть. Как насчет партии в шахматы?

Против стратегии с удвоением ставки есть замечательный прием (и он во всех казино используется) — именно, максимальный размер ставки. И все.

Осталось только понять, когда тормозить удвоение.. Пока стоит ограничение на 6 удвоений.
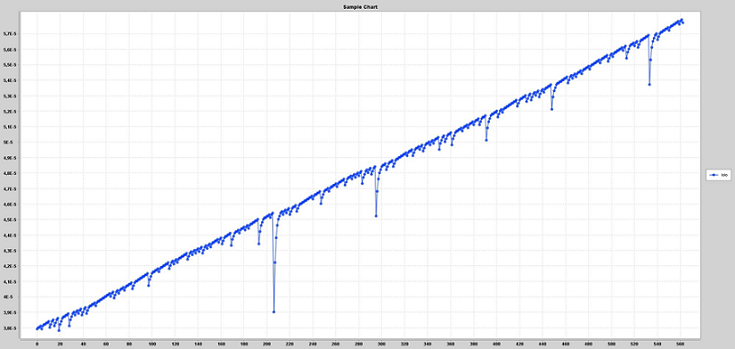
Вот так могут выглядеть возможные исходы (по вертикальной оси бюджет, по горизонтальной порядковый номер ставки)
Вот, когда все идет хорошо:


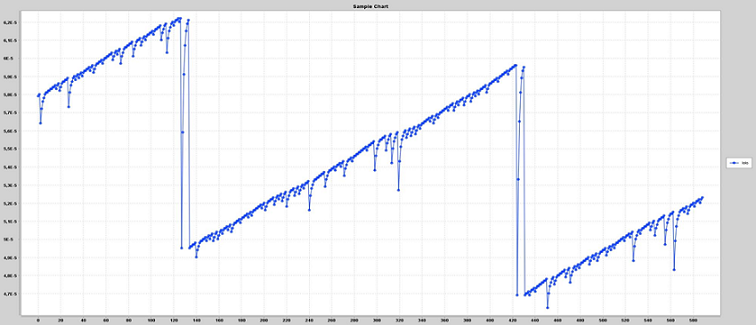
А вот бывают ситуации, когда не очень:


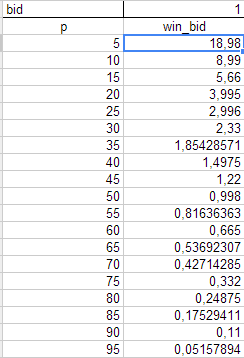
Что касается зависимости выигрыша от вероятности, то тут так: Делаю ставку равную 1 и в зависимости от вероятности (p) получаю определенyую сумму при выигрыше (win_bid)

[Евгений Машеров]

Тормозить удвоение лучше всего до начала игры. Вообще не приступая.
Из тайного математического открытия 0=0 следует, что если нет ни комиссии, ни подкрутки со стороны сервера, то за достаточно длинный период выигрыш будет равен проигрышу. А поскольку разработчикам сервера надо на что-то жить, то подкрутка более чем вероятна.
При честной игре, когда вероятности выигрыша и проигрыша равны 0.5, матожидание выигрыша при любой ставке 0. Соответственно, 0 при любой стратегии ставок. Сумма нулей - ноль. Тот факт, что ставка хитрым образом зависит от имеющегося выигрыша и, следовательно, ставки и выигрыши в данной партии могут быть не независимы, несущественен. Поскольку матожидание суммы равно сумме матожиданий и для зависимых величин.
То, что мартингейл позволяет сделать вероятность проигрыша сколь угодно малой, на общий выигрыш в действительно длинной серии не повлияет. Но позволит получить достаточно длинную прибыльную серию, чтобы убедить самого себя, что я перехитрил казино. Реальное казино перехитрить бывает сложнее.

[kp9r4d]

hello19
Да, вроде везде сделано так, что $p \cdot \operatorname{\text{win\_bid}}-(1-p) \cdot 1 \approx 0$, так что действительно никак… Скорее всего, именно в этом вам и предлагалось разобраться.